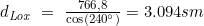Ausgehend von einem Abfahrtsort soll mit einem vorgegebenen Kurs ein bestimmter Breitengrad erreicht werden. Gesucht ist die Distanz und der Längengrad, an dem der Breitengrad erreicht wird.

Vorgehen wie folgt:
- Für die geographischen Breiten von Anfangsort φA und Bestimmungs-Breite φB werden die Vergrößerten Breiten ΦA und ΦB bestimmt:
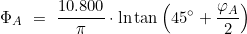
und
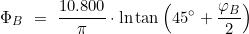
- Dann wird die Differenz ΔΦ der vergrößerten Breiten bestimmt:
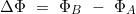
- Das Meridianabstandsverhältnis l* ergibt sich zu:
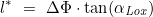
(l* in Winkelminuten)
Der Längenunterschied ergibt sich zu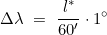
(Δλ in Grad)
- Für die Länge des Bestimmungsorts λB ergibt sich:
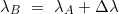
- Bestimmung des Breitenunterschiedes Δφ in Grad:
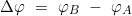
und b in Winkelminuten:
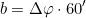
- Bestimmung der loxodromischen Distanz dLox:
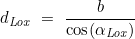
Du stehst nahe Gran Canaria auf 26° N und 16° W und willst Barabados auf 13° 13′ N und 59° 30′ W erreichen.
Deine Route soll zunächst mit Kurs 240° bis Breitengrad 13° 13’N führen und von dort genau westwärts.
Auf welcher Position erfolgt die Kursänderung von 240° auf 270°, welche Distanz ist vom Ausgangsort bis zum Punkt der Kursänderung zurückzulegen?
(Diese Aufgabenstellung ist dem Buch „Transatlantik in die Sonne“ von Bobby Schenk entnommen)
- Berechnung der Vergrößerten Breiten:
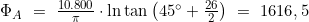

- Differenz ΔΦ der vergrößerten Breiten:

- Meridianabstandsverhältnis l*:
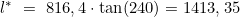
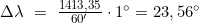
- Länge des Bestimmungsorts λB:
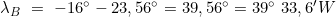
- Breitenunterschiedes Δφ:

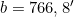
- loxodromischen Distanz dLox: