Erste Aufgabe der Besteckrechnung nach Vergrößerter Breite

Abfahrtsort (φ_A, λ_A), Kurs α_Lox und Distanz d_Lox sind gegeben,
der Bestimmungsort (φ_B, λ_B) wird gesucht.

Zunächst wird wie beim Mittelbreitenverfahren die Breitendistanz b errechnet:
$\begin{equation*} b\ =\ d_{Lox}\cdot \cos (\alpha _{Lox}) \end{equation*}$

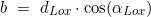
und Umrechnung in Grad

$\begin{equation*} \Delta \varphi\ =\ \frac{b}{60'} \end{equation*}$
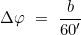
dann wird die geographische Breite des Bestimmungsortes φ_B errechnet:
$\begin{equation*} \varphi _{B}\ =\ \varphi _{A}+\Delta \varphi \end{equation*}$

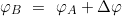
bei Fahrt über den Äquator:

$\begin{equation*} \varphi _{B}\ =\ \varphi _{A}-\Delta \varphi \end{equation*}$
Für die geographischen Breiten φ_A und φ_B werden die Vergrößerten Breiten Φ_A und Φ_B errechnet:
$\begin{equation*} \Phi _{A}\ =\ \frac{10.800}{\pi }\cdot \ln \tan \left(45{}^{\circ}+\frac{\varphi _{A}}{2}\right) \end{equation*}$

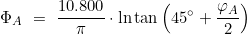
und

$\begin{equation*} \Phi_{B}\ =\ \frac{10.800}{\pi }\cdot \ln \tan \left(45{}^{\circ}+\frac{\varphi _{B}}{2}\right) \end{equation*}$
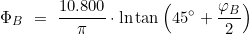
Aus den Vergrößerten Breiten wird der BreitenunterschiedΔΦ berechnet
$\begin{equation*} \Delta \Phi \ =\ \Phi _{B}\ -\ \Phi _{A} \end{equation*}$
Das Meridianabstandsverhältnis l^* ergibt sich in Winkelminuten zu:
$\begin{equation*} l^{\mathit{*}}\ =\ \Delta \Phi \cdot \tan (\alpha_{\mathit{Lox}}) \end{equation*}$

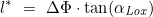
Der Längenunterschied Δλ ergibt sich in Grad zu:

$\begin{equation*} \Delta \lambda\ =\ \frac{l^{\mathit{*}}}{60\text{{\textquotesingle}}}\cdot 1{}^{\circ} \end{equation*}$
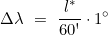
Für die geographische Länge des Bestimmungsortes ergibt sich:
$\begin{equation*} \lambda _{B}\ =\ \lambda _{A}+\Delta \lambda \end{equation*}$

bei Fahrt über den Äquator:

$\begin{equation*} \lambda _{B}\ =\ \lambda _{A}-\Delta \lambda \end{equation*}$

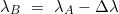
Die Ermittlung der Vergößerten Breiten kann auch nach einer Tabelle erfolgen.

Man segelt aus der Lübecker Bucht (φ_A = 54° 00,0′ N, λ_A = 010° 50,0′ E) mit einem Kurs = 060° eine Distanz von 160 sm.

Wie lauten die Koordinaten des Bestimmungsortes?

Berechnung nach Verfahren der vergrößerten Breite:

Berechnung der Breitendistanz
$b\ =\ d\cdot \cos (\alpha _{\mathit{Lox}})\ =\ 160\cdot \cos(60{}^{\circ})=80\text{{\textquotesingle}}$
$\Delta \varphi \ =\ \frac{b}{60\text{{\textquotesingle}}}\cdot 1{}^{\circ}\ =\ \frac{80}{60}\ =\ 1,333{}^{\circ}\ =\ 1{}^{\circ}20\text{{\textquotesingle}}$
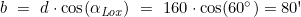
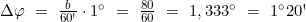
Berechnung der geographischen Breite des Bestimmungsortes φ_B
$\varphi _{B}\ =\ \varphi _{A}+\Delta \varphi\ =\ 54{}^{\circ}00,0\text{{\textquotesingle}}N+1{}^{\circ}20\text{{\textquotesingle}}\ =\ 55{}^{\circ}20\text{{\textquotesingle}}N$
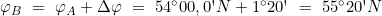
Berechnung der Vergrößerten Breiten Φ_A und Φ_B
$\Phi _{A}\ =\ \frac{10.800}{\pi }\cdot \ln \tan\left(45{}^{\circ}+\frac{\varphi _{A}}{2}\right)\ =\ \frac{10.800}{\pi}\cdot \ln \tan \left(45{}^{\circ}+\frac{54}{2}\right)\ =\ 3.864,6$
$\Phi _{B}\ =\ \frac{10.800}{\pi }\cdot \ln \tan\left(45{}^{\circ}+\frac{\varphi _{B}}{2}\right)=\frac{10.800}{\pi}\cdot \ln \tan \left(45{}^{\circ}+\frac{55,33}{2}\right)\ =\ 4.003,0$
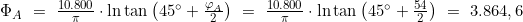
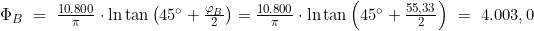
Berechnung des Breitenunterschiedes ΔΦ
$\Delta \Phi \ =\ \Phi _{B}\ -\ \Phi_{A}\ =\ 4.003\ -\ 3.864,6\ =\ 138,4$
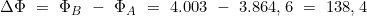
Berechnung des Meridianabstandsverhältnisses l^* und des Längenunterschiedes Δλ
$l^{\mathit{*}}\ =\ \Delta \Phi \cdot \tan (\alpha_{\mathit{Lox}})\ =\ 138,4\cdot \tan(60{}^{\circ})\ =\ 239,7\text{{\textquotesingle}}$
$\Delta \lambda\ =\ \frac{l^{\mathit{*}}}{60\text{{\textquotesingle}}}\cdot 1{}^{\circ}\ =\ \frac{239,7\text{{\textquotesingle}}}{60\text{{\textquotesingle}}}\cdot 1{}^{\circ}\ =\ 3,995{}^{\circ}\ =\ 3{}^{\circ}59,7\text{{\textquotesingle}}$
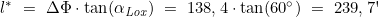
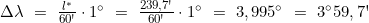
Berechnung der geographischen Länge des Bestimmungsortes
$\lambda _{B}\ =\ \lambda _{A}+\Delta \lambda\ =\ 10{}^{\circ}50\text{{\textquotesingle}}E+3{}^{\circ}59,7\text{{\textquotesingle}}\ =\ 14{}^{\circ}49,7\text{{\textquotesingle}}E$

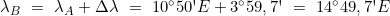
Die Koordinaten des Bestimmungsortes lauten:

$\varphi _{B}\ =\ 55^{\circ}\ 20'N$ und $\lambda _{B}\ =\ 014^{\circ} 49,7'E$

Post Views: 204