Großkreisrechnung

Seiteninhalt

Der kürzeste Weg von einem Abfahrtsort A zu einem Bestimmungsort B führt über einen Großkreis.

Großkreise sind Kreise auf der Erdoberfläche, deren Mittelpunkt durch den Erdmittelpunkt gehen; der Umfang aller Großkreise ist gleich dem Umfang des Äquators – der auch ein Großkreis ist.

Für alle Großkreise gilt: 1° entspricht 60sm, da eine Bogenminute einer Seemeile entspricht.

Die Berechnungen für Großkreisfahrt leiten sich aus der sphärischen Trigonometrie ab.

Das terrestrisch-sphärische Grunddreieck:

Für alle Großkreise gilt: 1° entspricht 60sm, da eine Bogenminute einer Seemeile entspricht.

Die Berechnungen für Großkreisfahrt leiten sich aus der sphärischen Trigonometrie ab.

Das terrestrisch-sphärische Grunddreieck:

Die Punkte A und B sind Abfahrts- bzw. Bestimmungsort, Punkt P_N ist der (Nord-) Pol, Punkt S ist der Scheitelpunkt (Punkt des maximalen Breitengrads).

Die Seite c bezeichnet die zurückzulegende Distanz auf dem Großkreis in Grad; wird auch als Winkel Δσ auf dem Großkreis bezeichnet.

Die Winkel α und β und sind die Innenwinkel des Dreiecks.

Der Scheitelpunkt muss nicht immer im Dreieck liegen; er liegt außerhalb, wenn einer der Innenwinkel α oder β stumpf ist.(d.h. größer 90°)

In der Praxis heißt das, entweder Abfahrts- oder Bestimmungsort liegen auf einem Breitengrad, der während der Fahrt von A nach B nicht überschritten wird.

In dem terrestrisch-sphärischen Grunddreieck gilt:

$a~=~90{}^{\circ}-\varphi_{B}$

$\lambda_{B}~=~\lambda_{A}+\Delta \lambda$

$b~=~90{}^{\circ}-\varphi_{A}$

$\lambda_{S}~=~\lambda_{A}+\Delta \lambda_{\mathit{AS}}$

$h~=~90{}^{\circ}-\varphi_{S}$

$\lambda_{S}~=~\lambda_{B}+\Delta \lambda_{\mathit{BS}}$

Großkreisanfangskurs und -endkurs leiten sich aus der Betrachtung der Innenwinkel α und β ab.

Bei Großkreissegelung in östliche Richtung ergeben sich Großkreis-Anfangskurs α_AK und Großkreis-Endkurs α_EK nach:

$\alpha _{\mathit{AK}}\ =\ \alpha$ und $\alpha _{\mathit{EK}}\ =\ 180{}^{\circ}~-~\beta$

und bei Großkreissegelung in westliche Richtung nach:

$\alpha _{\mathit{AK}}\ =\ 360{}^{\circ}-\alpha$ und $\alpha _{\mathit{EK}}\ =\ 180{}^{\circ}~+~\beta$

Berechnung der navigatorisch relevanten Größen

Jetzt wird es sehr mathematisch – aber lasse Dich von den Formeln nicht abschrecken.

Es gibt immer den ein oder anderen, der es genauer wissen will.

Wer einfach nur die fertigen Formeln anwenden möchte, überliest diese Absätze und schaut sich nur die eingerahmte Ergebnisformel am Ende an.

Berechnung der orthodromischen Distanz d_GK

Nach dem Seitenkosinussatz im sphärischen Dreieck gilt:

$\begin{equation*} \cos (c)\ =\ \cos (a)\cdot \cos (b)+\sin (a)\cdot \sin (b)\cdot \cos(\Delta \lambda ) \end{equation*}$

Für das Terrestrisch-sphärische Grunddreieck der Erde gilt:

$\begin{equation*} \boxed{\cos (c)\ =\ \sin (\varphi _{A})\cdot \sin (\varphi _{B})+\cos(\varphi _{A})\cdot \cos (\varphi _{B})\cdot \cos (\Delta \lambda )} \end{equation*}$

Die Distanz d_GK in Seemeilen erhält man, indem der Winkelwert c mit 60sm multipliziert wird:

$\begin{equation*} \boxed{d_{\mathit{GK}}\ =\ \frac{c}{1{}^{\circ}}\cdot 60\mathit{sm}} \end{equation*}$

Berechnung von Anfangs- und Endkurs

Der sphärische Sinussatz sagt aus:

$\begin{equation*} \cos (a)\ =\ \cos (b)\cdot \cos (c)+\sin (b)\cdot \sin (c)\cdot \cos(\alpha ) \end{equation*}$

bzw.

$\begin{equation*} \cos (\alpha )\ =\ \frac{\cos (a)-\cos (b)\cdot \cos (c)}{\sin(b)\cdot \sin (c)} \end{equation*}$

Für die Innenwinkel zur Berechnung der Anfangs- und Endkurse der Erdkugel gilt demnach:

$\begin{equation*} \boxed{\cos (\alpha )\ =\ \frac{\sin (\varphi _{B})-\sin (\varphi _{A})\cdot \cos (c)}{\cos (\varphi _{A})\cdot \sin (c)}} \end{equation*}$

$\begin{equation*} \boxed{\cos (\beta )\ =\ \frac{\sin (\varphi _{A})-\sin (\varphi _{B})\cdot \cos (c)}{\cos (\varphi _{B}) \cdot \sin (c)}} \end{equation*}$

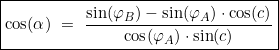
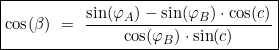
Fahrt in östliche Richtung:

$\alpha _{\mathit{AK}}\ =\ \alpha$

$\alpha _{\mathit{EK}}\ =\ 180{}^{\circ}~-~\beta$

Fahrt in westliche Richtung:

$\alpha _{\mathit{AK}}\ =\ 360^{\circ}-\alpha$

$\alpha _{\mathit{EK}}\ =\ 180{}^{\circ}~+~\beta$

Berechnung des Scheitelpunktes

Der Scheitelpunkt eines Großkreises ist der polnächste Punkt (also der Punkt mit Scheitelpunkt der maximalen Breite).

Im sphärischen Dreieck gilt (Napiersche Regel):

$\begin{equation*} \sin (h)\ =\ \sin (b)\cdot \sin (\alpha )\ =\ \sin (a)\cdot \sin(\beta ) \end{equation*}$

Für die Erdkugel gilt demnach:

$\begin{equation*} \boxed{cos (|\varphi _{S}|)\ =\ \cos (\varphi _{A})\cdot \sin (\alpha)\ =\ \cos (\varphi _{B})\cdot \sin (\beta )} \end{equation*}$

φ_S gleichnamig mit φ_A bzw. φ_B.

Den Längenunterschied berechnet man nach:

$\begin{equation*} \cos (b)\ =\ \cot (\alpha )\cdot \cot (\Delta \lambda _{\mathit{AS}}) \end{equation*}$

oder

$\begin{equation*} \cos (a)\ =\ \cot (\beta )\cdot \cot (\Delta \lambda_{\mathit{BS}}) \end{equation*}$

Die Gleichungen lauten nach Umstellung:

$\begin{equation*} \tan (|\Delta \lambda _{\mathit{AS}}|)\ =\ \frac{1}{\cos (b)\cdot \tan(\alpha )} \end{equation*}$

und

$\begin{equation*} \tan (|\Delta \lambda_{\mathit{BS}}|)\ =\ \frac{1}{\cos (a)\cdot \tan (\beta )} \end{equation*}$

und für die Erdkugel:

$\begin{equation*} \boxed{\tan (|\Delta \lambda _{\mathit{AS}}|)\ =\ \frac{1}{\sin (\varphi_{A})\cdot \tan (\alpha )}} \end{equation*}$

und

$\begin{equation*} \boxed{\tan (|\Delta \lambda_{\mathit{BS}}|)\ =\ \frac{1}{\sin (\varphi _{B})\cdot \tan (\beta )}} \end{equation*}$

$\lambda _{S}\ =\ \lambda _{A}+\Delta \lambda_{\mathit{AS}}$ bzw. $\lambda _{S}\ =\ \lambda _{B}+\Delta \lambda_{\mathit{BS}}$

Im Grunde genommen hat ein Großkreis immer zwei Scheitelpunkte:

Ein Scheitelpunkt liegt auf der Nordhalbkugel und ein Scheitelpunkt liegt auf der Südhalbkugel. (ausgenommen der Erdäquator, der auch ein Großkreis ist)

Die Koordinaten des zweiten Scheitelpunktes sind leicht zu ermitteln:

$\begin{equation*} \varphi _{\mathit{S2}}\ =\ -\ \varphi _{\mathit{S1}} \end{equation*}$

Also: liegt der erste Scheitelpunkt auf 45°N, dann liegt der zweite Scheitelpunkt auf 45° S.

$\begin{equation*} \lambda _{\mathit{S2}}\ =\ \lambda _{\mathit{S1}}\pm 180{}^{\circ} \end{equation*}$

Für die Äquatorschnitte gilt:

$\begin{equation*} \lambda _{\mathit{EQ1},2}\ =\ \lambda _{\mathit{S1}}\pm 90{}^{\circ} \end{equation*}$

und natürlich $\varphi _{\mathit{EQ1},2}\ =\ 0{}^{\circ}$

Berechnung der Meridianschnitte φ_M und λ_M

Ein Meridianschnitt ist ein Punkt auf dem Großkreis mit vorgegebenem Längengrad.

Zur Berechnung von Meridianschnitten wählt man Längengrade λ_M vor und berechnet die dazugehörigen Breiten φ_M.
Für die Berechnung der Meridianschnitte sind die Koordinaten des Scheitelpunktes φ_S und λ_S notwendig.

Meridianschnitte können einerseits benutzt werden, um einen Ausschnitt des Großkreises in eine Seekarte einzuzeichnen, sie eignen sich andererseits auch zum Planen einer Route mit kürzeren kursgleichen Abschnitten, die wie Sekanten eines
Kreises von einem Punkt auf dem Großkreis zum nächsten führen.

Der Längenunterschied zum Scheitelpunkt beträgt:

$\begin{equation*} \Delta \lambda _{\mathit{SM}}\ =\ \lambda _{M}-\lambda _{S} \end{equation*}$

Die Breite für den Meridianschnitt findet man über

$\begin{equation*} \tan (\varphi _{M})\ =\ \cos (\Delta \lambda _{\mathit{SM}})\cdot \tan(\varphi _{S}) \end{equation*}$

Der tangentiale Großkreiskurs in diesem Meridianschnitt berechnet sich als quadrantaler Kurs nach:

$\begin{equation*} \alpha \ =\ \arcsin \left(\frac{\cos (\varphi _{S})}{\cos (\varphi_{M})}\right) \end{equation*}$

Den vollkreisigen Kurs erhält man für

westliche Kurse:

$\alpha _{M}\ =\ 360{}^{\circ}-\alpha$ (Nordhalbkugel) bzw.
$\alpha _{M}\ =\ 180{}^{\circ}+\alpha$ (Südhalbkugel)

östliche Kurse:

$\alpha _{M}\ =\ \alpha$ (Nordhalbkugel) bzw.
$\alpha _{M}\ =\ 180{}^{\circ}-\alpha$ (Südhalbkugel)

Dieser tangentiale Kurs kann genutzt werden, wenn in einer Seekarte ein Ausschnitt eines Großkreises eingezeichnet werden soll.
Man bestimmt den Meridianschnitt und zeichnet dort den tangentialen Großkreiskurs an.

Werden die Meridianschnitte allerdings genutzt, um eine Großkreis-angenäherte Route mit kursgleichen Abschnitten zu konstruieren, so werden zunächst die Breitengrade der Meridianschnitte bestimmt.
Die Kurse α_1-2 zwischen jeweils zwei Meridianschnitten können dann durch die zweite Aufgabe der Besteckrechnung errechnet werden.
Dieser Kurs bildet mathematisch betrachtet eine Sekante innerhalb des Großkreises.

Näherungsweise Berechnung der Distanz bis zur nächsten Kursänderung um 1°

Da man auf dem Großkreis nicht ständig mit gelegtem Ruder exakt dem Kreis folgen wird, werden bestimmte Kurse gefahren.

Die Distanz bis zu der nächsten Kursänderung um 1° beträgt näherungsweise:

$\begin{equation*} d\ =\ \frac{60}{\tan (\varphi _{A})\cdot \sin (\alpha_{\mathit{AK}})}[\mathit{sm}] \end{equation*}$

Gradzahl einer Kursänderung nach einer Distanz mit vorgegebenen Seemeilen

$\begin{equation*} \Delta \alpha [{}^{\circ}]\ =\ \frac{d\cdot \tan (\varphi _{A})\cdot\sin (\alpha _{\mathit{AK}})}{60} \qquad d:~vorgegebene~Distanz~in~Seemeilen \end{equation*}$

Post Views: 167