Mittagslänge

Die Sonne kulminiert, wenn sie genau im Süden – auf der Südhalbkugel im Norden – steht.

Wenn die Sonne genau im Süden (bzw. im Norden) steht, folgt daraus, dass Beobachter und Bildpunkt auf einem Meridian sind.

Die Ungenauigkeiten wegen einer Eigenbewegung und zeitlicher Änderung der Deklination – so wie im Kapitel „Kulmination und Meridiandurchgang“ beschrieben, werden am Ende der Betrachtung berücksichtigt.

Wenn ich also zum Zeitpunkt der Kulmination den Meridian kenne, auf dem sich der Bildpunkt der Sonne befindet, kenne ich meine Länge.

Mit dem nautischen Jahrbuch ist es nicht sonderlich schwer, diesen Meridian herauszufinden; man sucht für den Zeitpunkt der Kulmination den Greenwichen Stundenwinkel der Sonne heraus – und schon ist die (westliche) Länge bekannt.

Es ist nur zu beachten, dass der Grt ja vollkreisig angegeben ist; das heißt GRT über 180° müssen von 360° abgezogen werden und ergeben dann östliche Längen.

Aber der Knackpunkt ist das genaue Feststellen des Kulminationszeitpunktes.

Dieser muss sehr genau bestimmt werden, denn jede Sekunde Abweichung vom genauen Zeitpunkt bedeutet eine Ungenauigkeit von 0,25 sm. Wird der Kulminationszeitpunkt um 1 min falsch bestimmt, ist die Länge um 15 sm daneben.

Da der Verlauf der Sonne im Bereich der Kulmination nur sehr flach verläuft, ist es schwierig, den genauen Zeitpunkt
festzustellen.

Man geht einen anderen Weg und bedient sich der Geometrie.

Verfahren der korrespondierenden Höhen

Der Verlauf der Sonne ist symmetrisch – wenn die Sonne also ca. 1 Stunde vor der errechneten Kulmination gemessen wird, bekomme ich einen bestimmten Wert h1 zu einem Zeitpunkt t1, der sich sekundengenau bestimmen lässt.

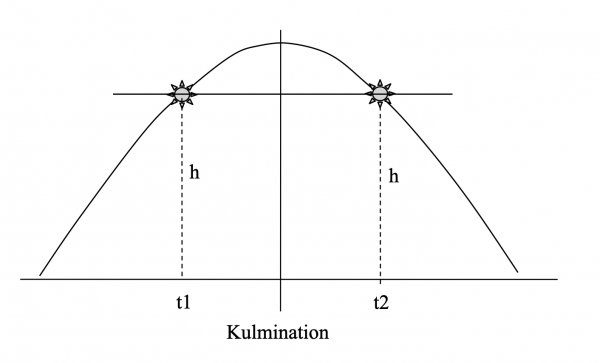
Nun wird eine Stunde nach der Kulmination wieder gemessen und der Zeitpunkt t2 bestimmt, an dem die Sonne wieder genau die Höhe h1 erreicht.

Dieser Zeitpunkt lässt sich genau bestimmen, da die Sonnenbahn nun wieder einen deutlichen Abwärtstrend hat.

Der Kulminationszeitpunkt liegt genau in der Mitte von t1 und t2 und lässt sich nun genau errechnen.

Mit diesem Wert ins Nautische Jahrbuch und den Greenwicher Stundenwinkel herausnehmen – und schon ist die Länge bestimmt:

Liegt Grt zwischen 000° und 180°: Westliche Länge λ = Grt

Liegt Grt zwischen 180° und 360°: Östliche Länge λ = 360° – Grt

Beispiel

Am 16. September 2005 wird die Sonne um 10.40.00 UT1 auf 48°10′ gemessen.
Diese Höhe stellt sich um 12.50.00 UT1 wieder ein.
Auf welcher Länge befinden wir uns ?
2. Zeitpunkt 12.50.00
– 1. Zeitpunkt 10.40.00
Zeitpunktunterschied 02.10.00
½ Zeitunterschied 01.05.00

 

1. Zeitpunkt 10.40.00
+ ½ Zeitunterschied 01.05.00
Zeitpunkt Kulmination 11.45.00

 

Grt11.00.00 346° 17,9′
+ Zuwachs 11° 15,0′
Grt11.45.00 357° 32,9′

Grt liegt zwischen 180° und 360° → λ = 360° – Grt; λ ist östlich.
Um besser subtrahieren zu können schreiben wir anstatt 360° 00,0′ den Wert 359° 60,0′, was das gleiche ist.

359° 60,0′
– Grt11.45.00 357° 32,9′
λ 002° 27,1′ E

In der Praxis wird man eine ganze Messreihe aufstellen. Denn stell Dir vor: Du misst die Sonnenhöhe vor der Kulmination und just zum Zeitpunkt nach der Kulmination, an dem sich die gleiche Sonnenhöhe einstellen soll, schiebt sich eine Wolke vor die Sonne.

Dann bleiben noch genug andere Messungen; mit einer wird es schon klappen den korrespondierenden Zeitpunkt nach Kulmination zu finden.

Fahrt zwischen den Messungen

Wenn das Fahrzeug zwischen den beiden Messungen Fahrt macht, wird das Messergebnis ungenau.

Es muss eine Korrektur in Abhängigkeit des Kurses angebracht werden:

    \begin{equation*} \Delta t_{\mathit{Ku}}\ [']\ \approx \ \frac{12}{\pi }\cdot \left(v\cdot \cos (\mathit{Az}-\alpha )+\mathit{Unt}\right)\cdot |\left(\tan (\varphi )-\tan (\delta )\right)| \end{equation*}

mit Az = 180° oder 360°

    \begin{equation*} \mathit{Grt}_{\mathit{Meridiandurchgang}}\ =\ \mathit{Grt}_{\mathit{Ku}}+\Delta t_{\mathit{Ku}} \end{equation*}

Beispiel

Am 16. September 2005 wird die Sonne auf φ ≈ 35°N um 10.40.00 UT1 auf 48°10′ gemessen.
Diese Höhe stellt sich um 12.50.00 UT1 wieder ein.

Zwischen den beiden Messungen wird ein Kurs von 200° mit einer Geschwindigkeit von 8kn gefahren.

Auf welcher Länge befinden wir uns?

    \begin{equation*} \Delta t_{\mathit{Ku}}\ [']\ \approx \ \frac{12}{\pi }\cdot \left(v\cdot \cos (\mathit{Az}-\alpha )+\mathit{Unt}\right)\cdot |\left(\tan (\varphi )-\tan (\delta )\right)| \end{equation*}

    \begin{equation*} \Delta t_{\mathit{Ku}}\ [']\ \approx \ \frac{12}{\pi }\cdot \left(8\cdot \cos (180-200)+1,0\right)\cdot |\left(\tan (35)-\tan (2{}^{\circ}31')\right)|\approx 21,4' \end{equation*}

    \begin{equation*} \mathit{Grt}_{\mathit{Meridiandurchgang}}\ =\ \mathit{Grt}_{\mathit{Ku}}+\Delta t_{\mathit{Ku}}=357{}^{\circ}32,9'+21,4=357{}^{\circ}54,3' \end{equation*}

    \begin{equation*} \lambda =002{}^{\circ}05,7'E \end{equation*}

Post Views: 210