Nebenmeridianbreite

Es kann vorkommen, dass die Sonne zum Kulminationszeitpunkt gerade hinter einer Wolke verschwindet – die Mittagsbreite kann in diesem Fall nicht gemessen werden.

Durch Messung der Sonne kurz vor oder auch kurz nach der Kulmination ist es mit dem Nebenmeridianbreiten-Verfahren aber auch möglich, eine Standlinie durch ein Breitenverfahren zu erhalten.

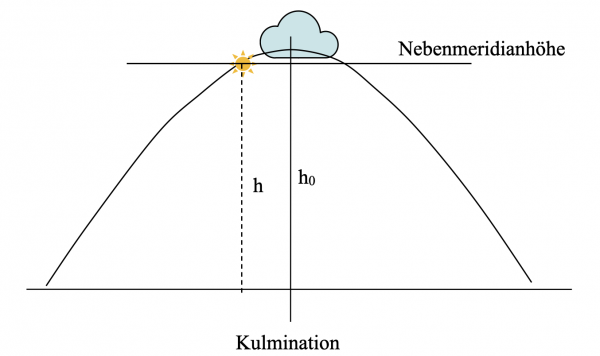
Bei einer Messung vor oder nach dem Kulminationszeitpunkt ist zu bedenken, dass eine zu niedrige Höhe hb als Meridianhöhe h0 gemessen wird und dass das Azimut nicht auf dem Meridian liegt sondern bei der Messung vor der Kulmination östlicher ist und bei der Messung nach der Kulmination westlicher ist.

Bei Sonne im Südmeridian ist das Azimut demnach vor dem Kulminationszeitpunkt kleiner als 180°, nach dem Kulminationszeitpunkt größer als 180°.

Der Höhenunterschied Δh = h0 – hb kann näherungsweise nach folgender Formel berechnet werden:

    \begin{equation*} \Delta h\ [']\ \approx \ 120\cdot \arcsin \left(\sin ^2\left(\frac{t_{E,W}} 2\right)\cdot \frac{\cos (\varphi )\cdot \cos (\delta )}{\cos (h_b)}\right) \end{equation*}

mit tE, W: halbkreisiger Ortsstundenwinkel

Das halbkreisige Azimut Z wird näherungsweise berechnet nach:

    \begin{equation*} Z\ \approx \ -t_{E,W}\cdot \frac{\cos (\delta )}{\sin (\varphi -\delta )} \end{equation*}

Vorgehen

  1. Für den Zeitpunkt der Messung werden aus dem Nautischen Jahrbuch Deklination und Ortsstundenwinkel bestimmt.
    (minutengenau ist ausreichend)
  2. Berechnung des Höhenunterschiedes und des Azimuts nach den oben angeführten Formel
  3. Die Meridianhöhe h0 ergibt sich aus h0 = hb + Δh
  4. Aus dieser Meridianhöhe wird die Nebenmeridianbreite ermittelt (wie bei Mittagsbreite)
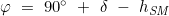    \varphi \ =\ 90{}^{\circ}\ +\ \delta \ -\ h_{\mathit{SM}} für Kulmination im Südmeridian
    \varphi \ =\ h_{\mathit{NM}}\ \ +\ \delta \ -\ 90{}^{\circ} für Kulmination im Nordmeridian
  5. Im Schnittpunkt Koppellänge / Nebenmeridianbreite wird der Azimutstrahl eingetragen; die Standlinie verläuft senkrecht dazu.
Beispiel:
Sie beobachten am 08.06.2005 kurz vor Meridiandurchgang um 12.50 UT1 auf 50°N, 17°W den Sonnenunterrand in einer Wolkenlücke. Sextantablesung 62° 28′, Ib=-2′, Ah=2m.
Bestimmen Sie die Meridianbreite und zeichnen Sie die Standlinie.
  1. Orstsstundenwinkel und Deklination
    Grt12.00.00 000° 14,4′
    + Zuwachs 12° 30,5′
    Grt12.50 012° 44,9′
    Grt12.50 372° 44,9′
    – λ – 017° 00,0′ („-“ da Westlänge)
    t 355° 44,9′

     

    359° 60,0′
    – t 355° 44,9′
    tW 004° 15,1′

     

    δ 22° 53,0′ N
  1. Höhenunterschied und Azimut
    SA 62° 28,0′
    + Ib -2,0′
    KA 62° 26,0′
    + Gb 13,0′
    + Zb -0,2′
    hb 62° 38,8′

        \begin{equation*} \Delta h\ [']\ \approx \ 120\cdot \arcsin \left(\sin ^2\left(\frac{4{}^{\circ}15,1'} 2\right)\cdot \frac{\cos (50{}^{\circ})\cdot \cos (22{}^{\circ}53')}{\cos (62{}^{\circ}38,8')}\right)\ \approx \ 12,2' \end{equation*}

        \begin{equation*} Z\ \approx \ -4{}^{\circ}15,1'\cdot \frac{\cos (22{}^{\circ}53')}{\sin (50{}^{\circ}-22{}^{\circ}53')}\ \approx \ -8,6{}^{\circ} \end{equation*}

        \begin{equation*} \mathit{Az}\ =\ 180{}^{\circ}-8,6\ =\ 171,4{}^{\circ} \end{equation*}

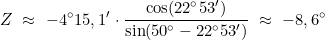
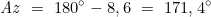
  1. Meridianhöhe h0

    hb 62° 38,8′
    + Δh 12,2′
    h0 62° 51,0′
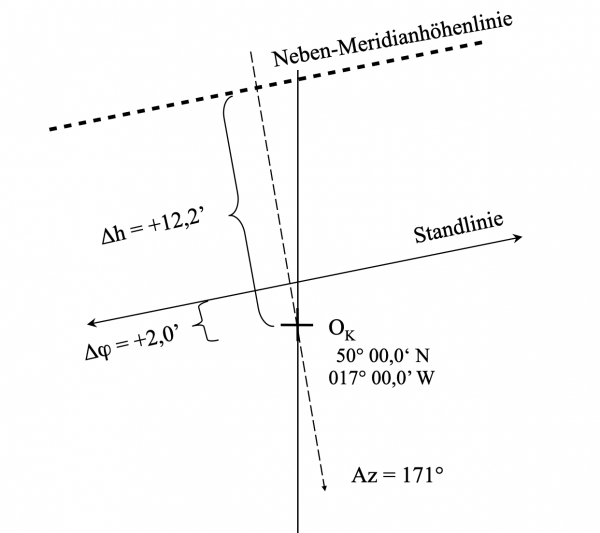
  1. Nebenmeridianbreite

        \begin{equation*} \varphi \ =\ 90{}^{\circ}\ +\ \delta \ -\ h_{\mathit{0}} \end{equation*}

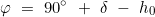
    90° 00,0′
    + δ + 22° 53,0′
    112° 53,0′
    – h0 62° 51,0′
    φB 50° 02,0′ N
    – φK 50° 00,0′ N
    Δφ 2,0′

Wie wir im Höhendifferenzverfahren sehen, kann dort auch eine Standlinie ähnlich dieser ermittelt
werden.

Ergebnis nach Höhendifferenzverfahren: Az=171,4°, Δφ= 1,8′

Wozu dann das Ganze mit der Nebenmeridianbreite?

Zugegeben – heute spielt die Nebenmeridianbreite keine Rolle mehr, da moderne Rechner die Lösung der aufwändigen Formeln des Höhendifferenzverfahrens leicht ermöglichen.

Zu Zeiten der Logarithmenrechnung war das Verfahren der Nebenmeridianbreite jedoch leichter und schneller zu rechnen als eine Höhenstandlinie nach dem Semiversusverfahren. Dabei wurden jedoch nicht die oben angeführten Formeln manuell gelöst sondern auf Tafelwerke zurückgegriffen – Nebenmeridiantafeln.

Es wurden verschiedene Nebenmeridiantafeln entwickelt, die die Berechnung vereinfachen.

Nebenmeridiantafeln aus Fulst Nautische Tafeln

Die Nebenmeridiantafeln im Tafelwerk Fulst Nautische Tafeln bestehen aus zwei Tafeln.

Tafel I tabelliert einen Faktor p für die Breite φ und die Deklination δ gemäß der Formel

    \begin{equation*} p\ = \frac {cos(\delta )} {sin(\varphi - \delta)} \end{equation*}

Dabei ist bei der Auswahl der richtigen Tabelle zu beachten, ob Breite und Deklination gleichnamig (also beispielsweise beide N oder S) oder ungleichnamig (ein Wert N, der andere S) sind.

    • Für halbkreisige Ortsstundenwinkel tE ergibt sich Azimut bei Gestirnen im Südmeridian:
      AZ = 180° – p * tE
    • Für halbkreisige Ortsstundenwinkel tW ergibt sich Azimut bei Gestirnen im Südmeridian
      AZ = 180° + p * tW

Mit der Tafel II wird die Meridianhöhe auf den Meridian korrigiert.

Dazu wird der Nebenmeridiantafel II mit der Breite und dem halbkreisigen Ortsstundenwinkel der Faktor q entnommen.

Die Tafelwerte sind nach der Formel

    \begin{equation*} q\ = \frac {2 \cdot sem(t_{E/W}) \cdot cos(\varphi)} {sin(1')} \end{equation*}

berechnet.

Die Winkeldistanz Δh in Minuten, die auf die gemessene Nebenmeridanhöhe zu addieren ist, um die Meridianhöhe zu erhalten, ist das Produkt aus p und q:

    \begin{equation*} \Delta h\ = p \cdot q \end{equation*}

Beispiel:
Sie beobachten am 08.06.2005 kurz vor Meridiandurchgang um 12.50 UT1 auf 50°N, 17°W den Sonnenunterrand in einer Wolkenlücke. Sextantablesung 62° 28′, Ib=-2′, Ah=2m.
Bestimmen Sie die Meridianbreite und zeichnen Sie die Standlinie.
  1. Bestimmung des halbkreisigen Ortstundenwinkels wie zuvor
    tw = 004° 15,1′ = 4,25°
  2. Bestimmung der Deklination δ wie zuvor
    δ = 22° 53′ N
  3. Bestimmung des Faktors p aus Nebenmeridiantafel I:
    φ und δ sind gleichnamig. (Beide N)
    p wird interpoliert für δ=22° (p=1,97) und δ=24° (p=2,08) zu
    p = 2,02
  4. Bestimmung Azimut
    Az = 180° – (p * tw) = Az = 180° – (2,02 * 4,25°)
    Az = 171,4°
  5. Bestimmung des Faktors q aus Nebenmeridiantafel II:
    q wird interpoliert für t=4° 10′ (q=5,8) und t=4° 20′ (q=6,3) zu
    q = 6,05
  6. Berechnung des Höhenunterschieds
    durch Multiplikation p * q = 2,02 * 6,05
    Δh = 12,2′
  1. Meridianhöhe h0

    hb 62° 38,8′
    + Δh 12,2′
    h0 62° 51,0′

Norie’s Ex-Meridian Tables

in den Norie’s Nautical Tables ist das Nebenmeridian-Verfahren mit drei Tabellen abgebildet; mit einer vierten kann validiert werden, ob die Messung eines Nebenmedidians noch im zulässigen Zeitrahmen liegt, da es ja nur ein Näherungsverfahren ist.

Analog zu den Fulst Nautischen Tafeln wird auch zunächst aus der Ex-Meridian Table I aus Länge und Deklination der Faktor A entnommen.

Dieser berechnet sich nach

    \begin{equation*} A\ =\ \frac{1,9635 \cdot cos(\varphi) \cdot cos(\delta)} {sin(\varphi - \delta)} \end{equation*}

Anschließend wird der Ex-Meridian Table II eine zweite Korrektur vorgenommen, die als Eingangswerte den Wert A sowie den Ortsstundenwinkel t hat.

Die Korrekturwerte werden für eine Ziffer von A angegeben; für Zehnerpotenzen und Nachkommastellen wird der Korrekturwert ebenfalls mit den Zehnerpotenzen multipliziert;
Ist A = 23,4, dann wird

  • der Wert unter „2“ genommen und mit zehn multipliziert
  • der Wert unter „3“ genommen
  • der Wert unter „4“ genommen und durch zehn geteilt

Der zweite Korrekturwert ist die Summe dieser Einzel-Summanden

Beispiel: φ = 24° N, δ = 16° N (Gleichnamig), t = 356°30′

A = 12,4

1: 3,3
2: 6,5
4: 13,1

Also ist die zweite Korrektur:

3,3 * 10 = 33,0
+ 6,5 * 1 = 6,5
+ 13,1 * 0,1 = 1,3
40,8

Das Azimuth ist über die ABC Tafeln zu bestimmen

A: Eingang Breite und Ortsstundenwinkel

B: Eingang Deklination und Ortsstundenwinkel

C (Azimut): Eingang (A+B) und Ortsstundenwinkel

Beispiel:
Sie beobachten am 08.06.2005 kurz vor Meridiandurchgang um 12.50 UT1 auf 50°N, 17°W den Sonnenunterrand in einer Wolkenlücke. Sextantablesung 62° 28′, Ib=-2′, Ah=2m.
Bestimmen Sie die Meridianbreite und zeichnen Sie die Standlinie.
  1. Bestimmung des Ortstundenwinkels wie zuvor
    t = 355° 45′
  2. Bestimmung der Deklination δ wie zuvor
    δ = 22° 53′ N
  3. Bestimmung des Wertes A aus der Ex-Meridian Table Ifür &phi=50°, δ=23°, gleichnamig (SAME) liest man ab:
    A = 2,6
  4. Bestimmung des ersten Korrekturwertes aus der Ex-Meridian Table IIfür t=355° 45′ liest man ab
    2: 9,6
    6: 28,9

    9,6 * 1 = 9,6
    + 28,9 * 0,1 = 2,9
    12,5
  5. Bestimmung des zweiten Korrekturwertes aus der Ex-Meridian Table III
    Für den ersten Korrekturwert „First Corr“ und der wahren Höhe 62° 38,8′ (Siehe oben) liest man ab:
    Second Corr = -0,1
  6. war Δ h beträgt somit 12,5 – 0,1 = 12,4 ‚
  1. Bestimmung des Azimut nach den ABC Tabellen
    A: φ=50° und t=355° 45′ ergeben A = 16,0
    B: δ=23° und t=355° 45′ ergeben B = 6,09
    C: A+B=22 und φ=50° ergeben C = 4°Azimut = 180° – 4° = 176°
Post Views: 330