Sichtweite eines Leuchtfeuers

Seiteninhalt

Feuer in der Kimm

Die (geographische) Sichtweite eines Feuers bezeichnet den Abstand in Seemeilen, in dem ein Feuer aus der Geometrie heraus in der Kimm sichtbar wird.

Die Sichtweite hängt in erster Linie von Feuerhöhe h_Fe und Augeshöhe Ah des Benutzers ab und kann durch die folgende Formel ermittelt werden:

$e\ \approx \ 2,075\cdot (\sqrt{h_{\mathit{Fe}}}+\sqrt{\mathit{Ah}})$

„Alter Hut, das habe ich doch schon im SKS gelernt! – Dort hieß das Feuer in der Kimm„

OK, wollen wir mal sehen, ob Du heute noch etwas neues zu diesem Thema lernst!

Wenn Du Dich mit der terrestrischen Navigation zum SSS oder SHS beschäftigst, wird das Thema wieder da sein. Neben der Lösung über die Formel bietet sich auch an, den Abstand aus einer Tabelle im Begleitbuch herauszulesen.

Die Tabelle ist mit „Geographical Range Table“ überschrieben und listet den Abstand zum Leuchtfeuer in Abhängigkeit zur Augeshöhe (horizontal in der Tabelle) und zur Feuerhöhe (vertikal in der Tabelle).

Wenn Du eine alte Ausgabe des Begleitheftes und Du die Werte der Tabelle schon einmal mit dem Formel-Wert verglichen hast, kann man mitunter Unterschiede sehen. Ich habe auch ein SKS Begleitheft vorliegen, wo das so war.

Die Tabellen sind zum Teil mit anderen Tabellen ersetzt worden.

Nehmen wir ein Beispiel:

Augeshöhe 5m, Feuerhöhe 20m; nach Formel ergibt sich ein Abstand von 13,92 sm.

Aus der Tabelle entnehmen wir 13,6 sm.

Geometrische Herleitung

Mit Erdradius, Augeshöhe und Feuerhöhe kann man unter Anwendung mathematischer Formeln (Satz des Pythagoras, Binomische Formeln) die Geometrische Sichtweite herleiten.

Wir betrachten die Verhältnisse in Form von rechtwinkligen Dreiecken:

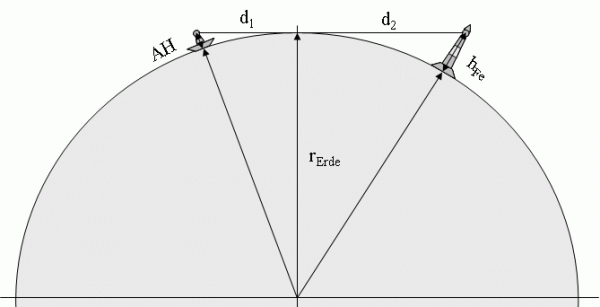
Das linke Dreieck ergibt sich mit den Eckpunkten Erdmittelpunkt – Auge des Betrachters – Kimm und den Seiten r_Erde, (r_Erde + Augeshöhe AH) und Abstand d₁.

Das rechte Dreieck ergibt sich mit den Eckpunkten Erdmittelpunkt – Feuer – Kimm und den Seiten r_Erde, (r_Erde + Feuerhöhe h_Fe) und Abstand d₂.

Im linken Dreieck gilt der Satz des Pythagoras

$r_{\mathit{Erde}}^2+d_1^2\ =\ (r_{\mathit{Erde}}+\mathit{AH})^2$

und nach d₁ aufgelöst:

$d_1\ =\ \sqrt{(r_{\mathit{Erde}}+\mathit{AH})^2-r_{\mathit{Erde}}^2}$

unter Anwendung der ersten binomischen Formel ergibt sich:

$\begin{equation*} d_1\ =\ \sqrt{(r_{\mathit{Erde}}^2+2\cdot r_{\mathit{Erde}}\cdot \mathit{AH}+\mathit{AH}^2)-r_{\mathit{Erde}}^2}\ =\ \sqrt{2\cdot r_{\mathit{Erde}}\cdot \mathit{AH}+\mathit{AH}^2} \end{equation*}$

Unter Berücksichtigung, dass der mittlere Erdradius gleich 6378 km ist und die Augeshöhe nur wenige Meter beträgt, kann der Summand AH² vernachlässigt werden, da er auf das Ergebnis nur einen geringen Einfluss hat.

$\begin{equation*} d_1\ \approx \ \sqrt{2\cdot r_{\mathit{Erde}}\cdot \mathit{AH}} \end{equation*}$

Um d₁ in Seemeilen zu erhalten, müssen auch r_Erde und AH in Seemeilen in die Formel eingehen.

$\begin{equation*} d_1\ \approx \ \sqrt{2\cdot \frac{6378}{1,852}\ \cdot \ \frac{\mathit{AH}[m]}{1852}}\ =\ \sqrt{3,719\cdot \mathit{AH}[m]}\ =\ 1,9285\cdot \sqrt{\mathit{AH}[m]} \end{equation*}$

Merken wir uns die letzte Formel und schauen ins rechte Dreieck. Die Verhältnisse sind exakt die gleichen – mit dem Unterschied, dass wir es hier anstatt der Augeshöhe AH mit der Feuerhöhe h_Fe zu tun haben. Daher sparen wir uns die analoge Herleitung und stellen fest:

$\begin{equation*} d_2\ \approx \ 1,9285\cdot \sqrt{h_{\mathit{Fe}}[m]} \end{equation*}$

Für die Gesamtdistanz (Geometrische Sichtweite) gilt:

$\begin{equation*} d_{\mathit{Geometrisch}}\ \approx\ d_1+d_2\ \approx \ 1,9285\cdot \sqrt{\mathit{AH}[m]}+1,9285\cdot \sqrt{h_{\mathit{Fe}}[m]} \end{equation*}$

$\begin{equation*} d_{\mathit{Geometrisch}}\ \approx\ 1,9285\cdot \left(\sqrt{\mathit{AH}[m]}+\sqrt{h_{\mathit{Fe}}[m]}\right) \end{equation*}$

Das sieht ja schon mal so ähnlich aus wie die allgemein bekannte Formel; nur der Faktor stimmt nicht!

Von der Geometrie zur tatsächlichen Sichtweite

Die geometrische Sichtweite beträgt nach der oben hergeleiteten Formel:

$\begin{equation*} d_{\mathit{Geometrisch}}\ \approx\ 1,9285\cdot \left(\sqrt{\mathit{AH}[m]}+\sqrt{h_{\mathit{Fe}}[m]}\right) \end{equation*}$

Unterschiedliche Temperatur und Luftdruckverteilungen in der Atmosphäre führen zu Schichtungen von Luftmassen unterschiedlicher Dichte. An diesen Schichten werden die Lichtstrahlen gebrochen und führen zu einer Krümmung („Terrestrische Refraktion“). Durch diese Bahnkurvenkrümmung kann man über die geometrische Sichtweite hinaus – quasi hinter den Horizont blicken.

Der Lichtstrahl folgt einem konvex verlaufenden Kreisbogen mit einem Radius, der näherungsweise dem achtfachen Erdradius entspricht.

In der Praxis kann man sagen, dass die tatsächliche Sichtweite etwa 5-8% größer ist als die geometrische Sichtweite.

Das BSH geht von einer tatsächlichen Sichtweite aus, die ca. 7,6% größer ist als die geometrische Sichtweite. Somit ergibt sich der Faktor zu $\ 1,076\cdot 1,9285\ = 2,075$

$\begin{equation*} d_{\mathit{Gesamt}}\ \approx \ 2,075\cdot \left(\sqrt{\mathit{AH}[m]}+\sqrt{h_{\mathit{Fe}}[m]}\right) \end{equation*}$

Das mag für die mittleren Witterungsverhältnisse in unseren Breiten zutreffen (was allerdings eine Vermutung des Autors ist)

International geht man nach einer Empfehlung der IALA davon aus, dass die tatsächliche Sichtweite im Mittel 5,3% größer ist als die geometrische Sichtweite. Hier Somit ergibt sich der Faktor zu $\ 1,053\cdot 1,9285\ = 2,03$

$\begin{equation*} d_{\mathit{Gesamt}}\ \approx \ 2,03\cdot \left(\sqrt{\mathit{AH}[m]}+\sqrt{h_{\mathit{Fe}}[m]}\right) \end{equation*}$

Diese Formel ist Basis der Geographical Range Table in den List of Light der British Admiralty!

Post Views: 406