Die zweite Aufgabe der Besteckrechnung dient dem Absetzen eines Kurses in der Seekarte. Demnach sind Abfahrtsort und Bestimmungsort bekannt, Kurs und Distanz sind gesucht.
Vorgehen wie folgt:
- Ermittlung des Breitenunterschieds Δφ
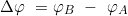
und Umrechnung in die Breitendistanz b

- Ermittlung des Längenunterschieds Δλ
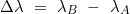
und Umrechnung in die Äquatormeridiandistanz l

- Ermittlung der Mittelbreite φM
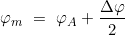
- Berechnung der Abweitung a
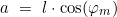
- Berechnung der loxodromischen Distanz d>Lox
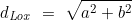
- Berechnung des quadrantalen Kurses α
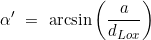
- Berechnung des loxodromischen Kurses αLox
- wenn
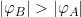 und
und 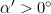 (I. Quadrant auf Nordhalbkugel)
(I. Quadrant auf Nordhalbkugel)

- wenn
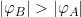 und
und 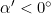 (IV. Quadrant auf Nordhalbkugel)
(IV. Quadrant auf Nordhalbkugel)
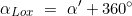
- wenn
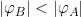 (II./III. Quadrant auf Nordhalbkugel)
(II./III. Quadrant auf Nordhalbkugel)
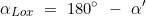
- wenn
Man steht in der Lübecker Bucht auf φA = 54° 00,0′ N, λA = 010° 50,0′ E und setzt Kurs auf einen Punkt nördlich Bornholm ab:
φB = 55° 20,0′ N, λB = 014° 49,7′ E
Wie lauten loxodromischer Kurs und Distanz?
Berechnung nach Mittelbreitenverfahren:
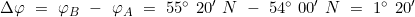
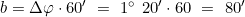
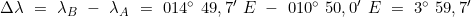
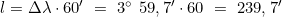

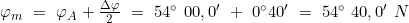
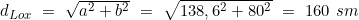
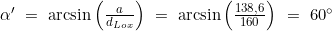
- I. Quadrant:
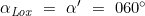
Loxodromischer Kurs: 060° Distanz: 160 sm.
