Beschickung der Höhenmessung

Seiteninhalt

Der Sextant liefert einen Winkel zwischen der sichtbaren Kimm und dem Gestirn. Dieser Winkel soll im folgenden Sextant-Ablesung SA genannt werden.
Wir müssen an diesem Wert einige Korrekturen anbringen, um die wahre Höhe des Gestirns zu erhalten.

Indexfehler

Der erste Messfehler ist wie zuvor beschrieben der Indexfehler.
Um aus der Sextantablesung SA den Kimmabstand KA, also dem richtigen Winkel zwischen Kimm und Gestirn, zu ermitteln, muss die Indexberichtigung Ib berücksichtigt werden. Damit ist der Nullpunkt-Fehler des Sextanten berücksichtigt.

Rechenmuster:

SA	51° 22,5′	Sextantablesung
Ib	+3,0′	Indexberichtigung
KA	51° 25,5′	Kimmabstand

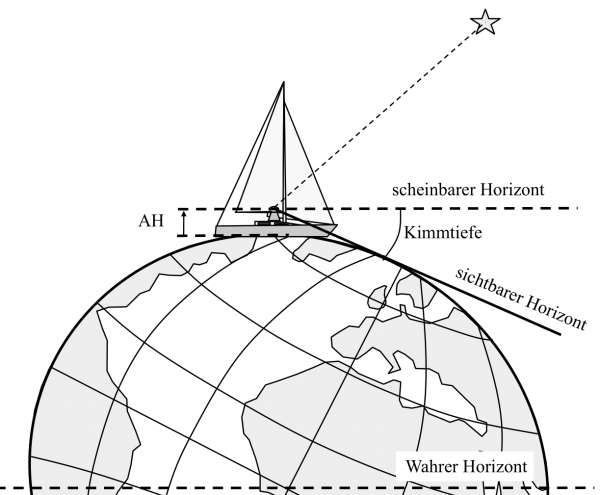
Kimmtiefe

Engl.: Dip of Horizon D

Je höher wir uns über über der Wasserlinie befinden, desto weiter können wir gucken.
Der sichtbare Horizont, die Kimm, wandert weiter von uns weg und der Winkel zwischen Gestirn und Kimm ist größer als der Winkel zum scheinbaren Horizont.

Die Augeshöhe Ah bewirkt, dass wir den sichtbaren und scheinbaren Horizont nicht gleichsetzen können. Der scheinbare Horizont verläuft auf der Höhe Ah senkrecht zum Lot zum Erdmittelpunkt, die Kimm ist um die Kimmtiefe Kt vergrößert.

Die scheinbare Höhe h_s ergibt sich zu

$h_s\ =\ \mathit{KA}-\mathit{Kt}$

Die mittlere Kimmtiefe lässt sich nach folgender Formel näherungsweise bestimmen:

$\begin{equation*} \mathit{Kt}\ \approx \ 1,78'\cdot \sqrt{\frac{\mathit{AH}}{[m]}} \end{equation*}$

(Herleitung dieser Formel siehe hier)

oder tabellarisch:

Bei einer auf Segelyachten üblichen Augeshöhe von 2 bis 2,5m beträgt die Kimmtiefe 2,5′ bis 2,8′ – runden wir großzügig auf 3′.

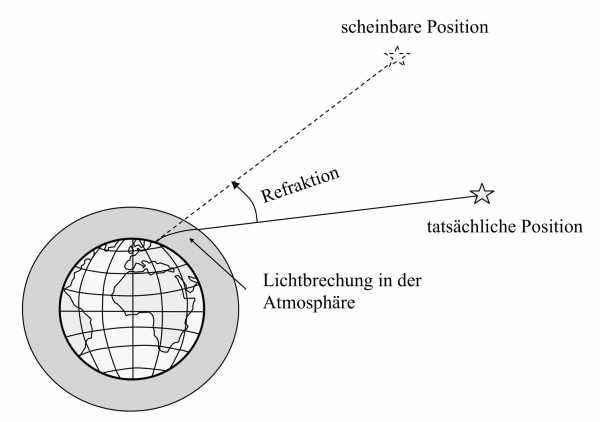
Refraktionsfehler

Als nächster Fehler kommt der Refraktionsfehler R hinzu; die parallelen Strahlen eines Gestirns werden durch die Atmosphäre zur Erde hin gebrochen.

Dem Beobachter scheinen die Gestirne in anderen scheinbaren Winkeln, als sie tatsächlich stehen.

Auch R lässt sich mit guter Näherung in einer Formel berechnen, die für eine Temperatur von 10°C, einem Normaldruck von 1013 hPa und einer Höhe h_s> 3° ihre Gültigkeit behält:

$\begin{equation*} R_0\ =\frac{1'}{\tan \left(h_s+\frac{7,31{}^{\circ}}{h_s+4,4{}^{\circ}}\right)} \end{equation*}$

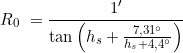
Für kleine Winkel gilt die Gleichung:

$\begin{equation*} R_0\ =\ \frac{34,1571+4,2\cdot h_s+0,004286\cdot h_s^2}{1+0,505\cdot h_s+0,0845\cdot h_s^2} \end{equation*}$

Bei anderen Luftdruck- und Temperaturverhältnissen muss die Formel für R₀ noch korrigiert werden:

$R\ =\ R_0\ \cdot \ \frac p{1013}\ \cdot \ \frac{283}{273+T}\ =\ 0,279\cdot \frac p{t+273{}^{\circ}}$

mit p: Druck in hPa und T: Temperatur in °C.

Die Höhe über dem scheinbaren Horizont h’ berechnet sich zu

$\begin{equation*} h'\ =\ h_s-R \end{equation*}$

Für Messungen im Zenit (h_S = 90°) ist die Refraktion 0°.

Für Messungen von Gestirnen im Wahren Horizont (=Auf- und Untergang) ist die Refraktion maximal und beträgt ca. 35′.

Höhenparallaxe / Horizontalparallaxe

Eine relativ kurze Distanz zwischen einem Gestirn und der Erde bewirkt einen Fehler durch Höhenparallaxe P, der daraus resultiert, dass die auf der Erde ankommenden Strahlen nicht mehr als parallel angenommen werden können.

Die Größe der Parallaxe ist abhängig von Entfernung des Gestirns zur Erde und der Höhe h’ über dem scheinbaren Horizont .

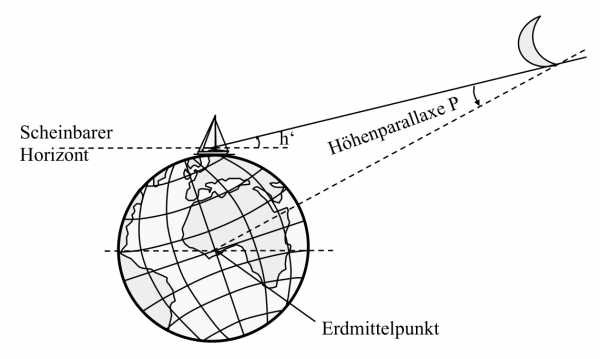
Steht das Gestirn im scheinbaren Horizont, ist der Fehler am größten. Die Parallaxe wird hier Horizontalparallaxe HP genannt.
(auch Horizontal-Verschub genannt)

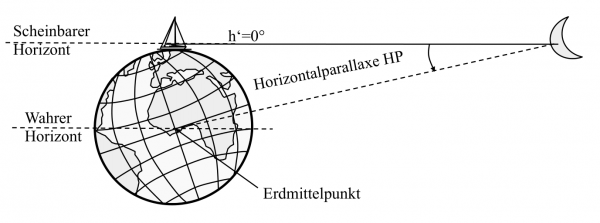
Steht es im Zenit, so ist der Fehler durch Höhenparallaxe = 0.

Insgesamt folgt der Fehler durch Höhenparallaxe P näherungsweise der Gleichung

$\begin{equation*} P\ =\ \mathit{HP}\cdot \cos (h') \end{equation*}$

Je weiter das Gestirn von der Erde entfernt ist, desto geringer wird der Fehler.

Die Fixsterne haben aufgrund ihrer großen Entfernung eine Horizontalparallaxe von HP=0′.
Für die Sonne liegt die Horizontalparallaxe zwischen HP =8” und 9”, für den Mond zwischen HP=54′ und 61′; die Planeten haben eine Horizontalparallaxe zwischen HP=0′ und 0.5′.

Die zutreffenden Werte können dem Nautischen Jahrbuch entnommen werden, sie sind unter den jeweiligen Spalten unter der Abkürzung HP zu finden. In der Praxis wird die Höhenparallaxe nur für den Mond und allenfalls für die Venus und Mars berücksichtigt.

Für den Mond ergibt sich ein Zusammenhang zwischen der Horizontalparallaxe und dem Monddurchmesser. Je näher der Mond an der Erde, desto größer die Horizontalparallaxe, desto größer der Monddurchmesser.

$\begin{equation*} d_{\mathit{Mond}}\ \approx \ 0,545867962\cdot \mathit{HP}\ \approx \ \frac 6{11}\cdot \mathit{HP} \end{equation*}$

Sonnen-/Mondradius

Sonne und Mond können nicht mehr als punktförmige Sterne angesehen werden. Dort müssen die Radien berücksichtigt werden. Eine Messung des jeweiligen Unterrandes zur Kimm scheint praktikabel.

Den Radius der Sonne kann man über

$r_{\mathit{Sonne}}\ =\ 16,0'+0,25'\cdot \cos (d)$ mit d=Anzahl der Tage im laufenden Jahr

näherungsweise bestimmen.

Der Radius des Mondes berechnet sich aus der Horizontalparallaxe HP wie oben angeführt zu

$\begin{equation*} r_{\mathit{Mond}}\ \approx \ 0,272\cdot \mathit{HP} \end{equation*}$

Je nach Messung des Unter- oder Oberrandes von Mond bzw. Sonne muss der Radius addiert bzw. subtrahiert werden.

Post Views: 99