Kimmtiefe

Seiteninhalt

Herleitung der Formel

Die Herleitung der Formel für die Kimmtiefe ist analog der Formel für Feuer in der Kimm.

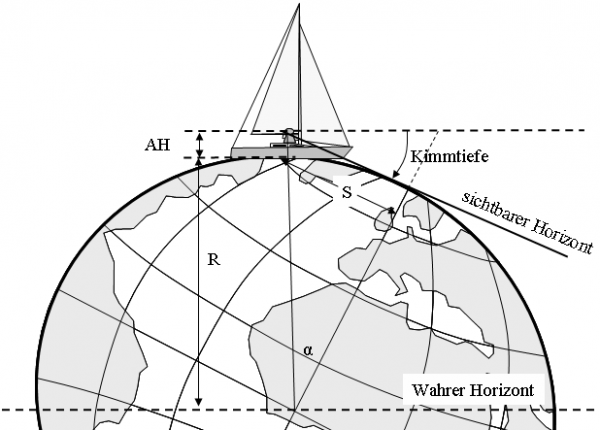
Für die Sichtweite S gilt:

$\begin{equation*} S\ =\ R\cdot \tan (\alpha ) \end{equation*}$

Da der Winkel sehr klein ist, kann man hier tan(α) ≈ α setzen (gilt für Winkel im Bogenmaß)
und α ist gleich Kimmtiefe Kt

Daraus ergibt sich:

$\begin{equation*} S\ \approx \ R\cdot \mathit{Kt} \end{equation*}$

Weiterhin gilt die Dreieckbeziehung:

$R^2+S^2\ =\ (R+\mathit{AH})^2$

bzw.

$\begin{equation*} R^2+(R\cdot \mathit{Kt})^2\ =\ (R+\mathit{AH})^2\mathit{bzw.}\ \ \ R^2(1+\mathit{Kt}^2)\ =\ (R+\mathit{AH})^2 \end{equation*}$

$\begin{equation*} \mathit{Kt}^2\ =\ \frac{R^2+2\cdot R\cdot \mathit{AH}+\mathit{AH}^2}{R^2}-1\ =\ \frac{2\cdot R\cdot \mathit{AH}+\mathit{AH}^2}{R^2} \end{equation*}$

Da AH² sehr klein im Verhältnis zu 2 R AH ist, wird dieser Summand vernachlässigt:

$\mathit{Kt}^2\ \approx \ \frac{2\cdot R\cdot \mathit{AH}}{R^2}\ =\ \frac 2 R\cdot \mathit{AH}$

bzw.

$\mathit{Kt}[\mathit{rad}]\ \approx \ \sqrt{\frac 2 R\cdot \mathit{AH}}\ =\ \sqrt{\frac 2 R}\cdot \sqrt{\mathit{AH}}$

Umrechnung vom Bogenmaß in Winkelminuten erfolgt über den Faktor $\frac{10.800}{\pi }$ :

$\mathit{Kt}[']\ \approx \ \frac{10.800}{\pi }\cdot \sqrt{\frac 2 R}\cdot \sqrt{\mathit{AH}}\ =\ 1,9261277\cdot \sqrt{\mathit{AH}}$

(rein geometrische Lösung!)

Unter Berücksichtigung, dass man aufgrund der terrestrischen Refraktion ca. 8\% weiter sehen kann, ergibt sich anstatt 1,93′ ein Faktor von 1,78′ und somit:

$\begin{equation*} \mathit{Kt}[']\ \approx \ 1,78\cdot \sqrt{\mathit{AH}} \end{equation*}$

Messung der Kimmtiefe

Die Kimmtiefe kann mit zenitnahen Gestirnen mittels eines genau gehenden Sextanten überprüft werden.

Das Gestirn wird zweimal gemessen:

Einmal wird der Kimmabstand KA₁ in Richtung des Gestirns gemessen.
(Spitzer Kimmabstand)
Bei der zweiten Messung wird in Gegenrichtung über der Zenit hinweg der Kimmabstand KA₂ gemessen.
(Stumpfer Kimmabstand)

Da ein Sextant maximal Winkel bis 120° messen kann, muss der KA1 entsprechend größer als 65° sein.

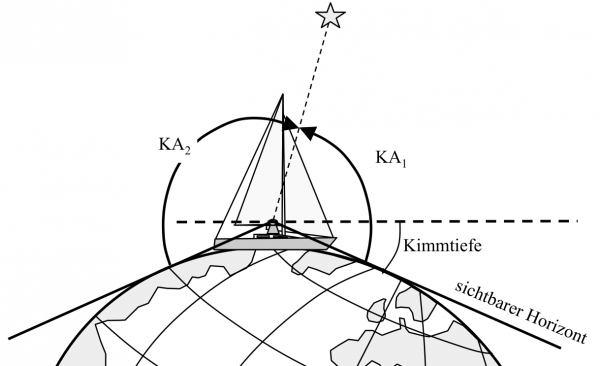
Bei der Summe dieser beiden Messungen wird die Kimmtiefe zweimal mit gemessen:

$\mathit{KA}_1+\mathit{KA}_2\ =\ 180{}^{\circ}+2\cdot \mathit{Kt}$

bzw.

$\mathit{Kt}\ =\ \frac{\mathit{KA}_1+\mathit{KA}_2-180{}^{\circ}} 2$

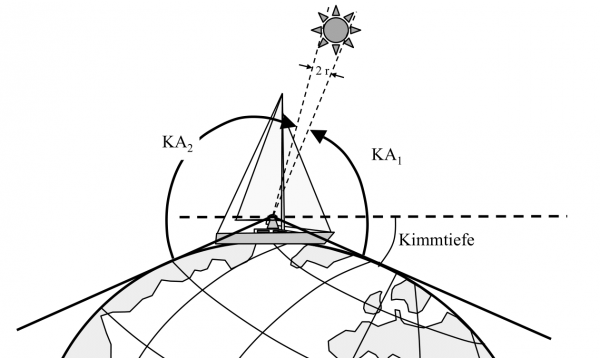
Wird die Sonne gemessen, so wird bei der spitzen Messung der Unterrand gemessen, bei der stumpfen der Oberrand, so dass man quasi zweimal den selben Rand misst.

$\mathit{KA}_1+\mathit{KA}_2+2\cdot r_{\mathit{Sonne}}\ =\ 180{}^{\circ}+2\cdot \mathit{Kt}$

bzw.

$\mathit{Kt}\ =\ \frac{\mathit{KA}_1+\mathit{KA}_2+2\cdot r_{\mathit{Sonne}}-180{}^{\circ}} 2$

Weiterhin müssen wir berücksichtigen, dass die Messungen mit einem bestimmten zeitlichen Versatz erfolgen werden, in dem sich die Höhe des Gestirns verändern wird:

$\Delta h_Z[']\ =\ 15\cdot \Delta t\cdot \sin (\mathit{Az})\cdot \cos (\varphi )$
mit

Δt Zeitunterschied zwischen den Messungen gemessen in Minuten,
Azimut Az
Breitengrad φ

Wenn zwischen den Messungen eine Distanz zurückgelegt wird, muss ebenso die Höhenänderung durch Versegelung berücksichtigt werden:

$\Delta h_V[']\ =\ \frac 1{60}\cdot \Delta t\cdot v\cdot \cos (\mathit{Az}-\mathit{K\text{ü}G})$
mit

Δt: Zeitunterschied zwischen den Messungen gemessen in Minuten,
v: Schiffsgeschwindigkeit in Knoten
Az: Azimut
KüG: Kurs über Grund

Der Kimmabstand KA₁ ist zu berichtigen:

$\mathit{KA}_1'\ =\ \mathit{Ka}_1+\Delta h_Z+\Delta h_V$

Post Views: 221