Höhenbeschickung mit dem Nautischen Jahrbuch des BSH

In der Praxis müssen wir uns nicht mit der Kenntnis all dieser Details herumschlagen – wir fassen die einzelnen Fehler aus Refraktion, Augeshöhe, Horizontalparallaxe und ggf. Gestirndurchmesser (bei Sonne und Mond) zusammen und sehen den entsprechenden Wert der Korrektur in einer Tafel nach.

Das Nautische Jahrbuch hält zu diesem Zweck Beschickungstafeln für Sonne, Mond und Planet/Fixsterne vor.

In den Beschickungstabellen sind jeweils mehrere Einzelverbesserungen zu einer Gesamtbeschickung Gb zusammengefasst. Eine Zusatzbeschickung berücksichtigt dann noch einen weiteren Ausgangswert.

Die Beschickungstabellen sind für die verschiedenen Himmelskörper unterschiedlich aufgebaut.

Die Berechnung von der Sextantablesung zur beobachteten Höhe hb erfolgt nach dem Rechenmuster:

SA Sextantablesung
+ Ib Indexberichtigung
KA Kimmabstand
+ Gb Gesamtbeschickung
+ Zb Zusatzbeschickung
hb Beobachtete Höhe

Sonne

Zur Bestimmung der Höhenbeschickung der Sonne müssen wir neben Augeshöhe und beobachteter Höhe auch noch den Sonnenradius sowie die Jahreszeit berücksichtigen.

Im Winter der Nordhalbkugel befindet sich die Erde auf ihrer elliptischen Umlaufbahn um die Sonne am sonnennächsten Punkt („Perihel“ am 3. Januar). Zu dieser Zeit ist die Sonnenscheibe am größten. (Radius ≈ 16,25′)Der sonnenfernste Punkt („Aphel“) ist am 5. Juli, zu dieser Zeit ist die Sonnenscheibe am kleinsten. (Radius ≈ 15,75′). Der Verlauf des Sonnenradius über das Jahr gesehen folgt einer Cosinus-Kurve.

Für eine Sonnenmessung liegt entweder die Messung des Sonnenunterrandes oder des Sonnenoberrandes zugrunde.

Die Tabelle für die Gesamtbeschickung geht von der Messung des Sonnenunterrandes bei einem mittleren Sonnenradius von 16,0′ aus.

Als Eingangsgrößen für die Gesamtbeschickung sind:

  • Augeshöhe

  • Kimmabstand

Bei der Sonne muss die Zusatzbeschickung je nach Messung des Ober- oder Unterrandes mit einbezogen werden. Der cosinusförmige Verlauf des Sonnenradius findet Eingang in die Tabelle „Zusatzbeschickung für den Kimmabstand des Sonnenunterrandes“ unterhalb der Gesamtbeschickungstabelle.

Kann der Sonnenunterrand aus irgendeinem Grund nicht gemessen werden (Wolken,…), ist die Zusatzbeschickungstabelle für den Sonnenoberrand zu wählen, deren Werte um den mittleren Sonnendurchmesser von 32′ vergrößert sind.

Die Beschickung der Sonne erhält man aus Addition von Gesamtbeschickung und Zusatzbeschickung.

  1. Berechne hb für die Beobachtung des Sonnenunterrandes am 11.06.2005 für SA=38° 12′ und Ib=-1′ und Ah=2m:

    SA 38° 12,0′
    + Ib -1,0′
    KA 38° 11,0′
    + Gb +12,4′ (1)
    + Zb -0,2′ (2)
    hb 38° 23,2′

    (1) Interpoliert zwischen 35° und 40°
    (2) für Monat Juni für den Unterrand

  2. Berechne hb für die Beobachtung des Sonnenoberrandes am 10.09.2005 für SA=48° 50′ und Ib=+2′ und Ah=3m

    SA 48° 50,0′
    + Ib +2,0′
    KA 48° 52,0′
    + Gb +12,2′ (1)
    + Zb -31,9′ (2)
    hb 48° 32,3′

    (1) Interpoliert zwischen KA=45° und 50° sowie Ah=2m und 4m
    (2) für Monat September für den Oberrand

Fixstern / Planet

Fixsterne und Planeten beobachten wir als punktförmige Gestirne, deren Durchmesser wir vernachlässigen können.

Die Bestimmung der Gesamtbeschickung ist hier besonders einfach; sie hängt nur ab von

  • Augeshöhe des Beobachters und

  • Kimmabstand.

Das nautische Jahrbuch beinhaltet eine Tabelle, aus der wir unter Berücksichtigung dieser Werte sofort die Gesamtbeschickung ablesen können.

Für erdnahe Planeten muss gegebenenfalls noch eine Zusatzbeschickung auf Grund der Horizontalparallaxe angebracht werden.

Der Kimmabstand wird um diesen Wert korrigiert, und man erhält die wahre Höhe.

  1. Berechne hb für die Beobachtung eines Fixsterns für SA=42° 44′ und Ib=0′ und Ah=2m

    SA 42° 44,0′
    + Ib 0,0′
    KA 42° 44,0′
    + Gb -3,6′ (1)
    + Zb
    hb 42° 40,4

    (1) Interpoliert zwischen 40° und 45°

  2. Berechne hb für die Beobachtung des Mars am 24.03.2005 für SA=50° 01′ und Ib=+1′ und Ah=2m

    SA 50° 01,0′
    + Ib +1,0′
    KA 50° 02,0′
    + Gb -3,3′
    + Zb +0,1′ (1)
    hb 49° 58,8′

    (1) für KA=50° und HP=0,2

Mond

Etwas komplizierter wird es mit der Bestimmung der Gesamtbeschickung des Mondes über Tafeln die Beschickungstafeln. Hier ist die Tabelle ganz anders aufgebaut:

Die Gesamtbeschickung wird bestimmt in Abhängigkeit von

  • Kimmabstand und

  • Horizontalparallaxe

Die Tafelwerte für die Gesamtbeschickung gilt für eine Augeshöhe Ah von 10m. Für andere Werte der Augeshöhe muss eine zusätzliche Berichtigung vorgenommen werden. Für Ah=2m sind beispielsweise jeweils 3,1′ hinzu zu zählen.

Wird der Mondoberrand gemessen, muss der Monddurchmesser, der unterhalb der Tabelle in Abhängigkeit zur Horizontalparallaxe aufgeführt ist, berücksichtigt werden.

Bei Messungen des Mondes kann es wegen der sichtbaren Mondscheibe vorkommen, dass nur der Oberrand sichtbar ist.

Um den Umfang der Tafeln auf zwei Seiten zu beschränken, ist es notwendig, viele Werte durch Interpolieren zu bestimmen.

Zunächst ist die Horizontalparallaxe, die im Nautischen Jahrbuch an jedem Kalendertag für 4h, 12h und 20h angegeben ist, für die entsprechende Zeit zu bestimmen – es wird zwischen zwei Zeiten interpoliert.

Als nächstes müssen vier Eckwerte aus der Tafel genommen werden.
Die vier Eckwerte ergeben sich aus den Kombinationen von jeweils kleinerem Kimmabstand mit kleinerem HP bis zu größerem Kimmabstand mit größerem HP.

Am besten verdeutlicht man diese kompliziert scheinende Rechnung an einem Beispiel:

Berechne hb für die Beobachtung des Mondoberrandes am 15.06.2005 um 18.45 UTC für SA=34° 20′ und Ib = -3′ und Ah=2m

  1. Bestimmung der Horizontalparallaxe

    Aus dem Nautischen Jahrbuch wird für den 15.06. aus der Spalte Mond, letzte Zeile entnommen:

    UT1 04 12 20
    HP 55,2′ 55,4′ 55,7′

    Für 18.45 muss also zwischen 12 und 20 UT1 interpoliert werden; die HP beträgt um 18.45:

        \begin{equation*} \mathit{HP}\ =\ 55,4+\frac{55,7-55,4} 8\cdot (18:45-12:00)\ =\ 55,4+0,0375\cdot 6,75\ =\ 55,65' \end{equation*}

        \begin{equation*} \mathit{HP}\ \approx \ 55,7' \end{equation*}

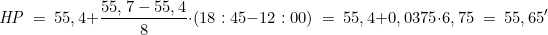
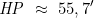
    Die Horizontalparallaxe nimmt mit der Zeit zu, d.h. der Abstand Erde/Mond verringert sich!

  2. Berechnung des Kimmabstandes

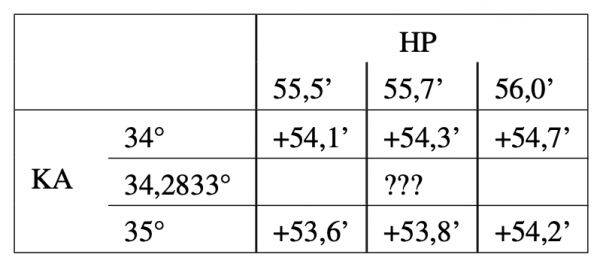
    SA 34° 20,0′
    + Ib -3,0′
    KA 34° 17,0′
  3. Ermittlung der Gesamtbeschickung abhängig von Kimmabstand und Horizontalparallaxe:Aus dem N.J. wird aus der „Gesamtbeschickungstafel für den Kimmabstand des Mondunterrandes“ entnommen: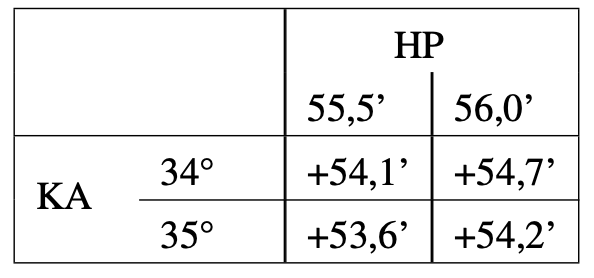Aus diesen vier Werten muss der richtige Wert für KA=34° 17′ und HP=55,7′ interpoliert werden.

    Dies geschieht in zwei Schritten – zunächst werden die Beschickungswerte für KA=34° und HP=55,7′ sowie KA=35° und HP=55,7′ durch Interpolation ermittelt:

        \begin{equation*} \mathit{GB}_1\ =\ 54,1+\frac{54,7-54,1}{56,0-55,5}\cdot (55,7-55,5)\ =\ 54,34\ \approx 54,3 \end{equation*}

        \begin{equation*} \mathit{GB}_2\ =\ 53,6+\frac{54,2-53,6}{56,0-55,5}\cdot (55,7-55,5)\ =\ 53,84\ \approx 53,8 \end{equation*}

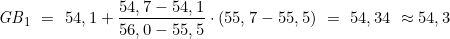
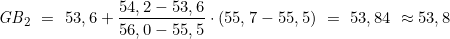
    Nun wird die Gesamtbeschickung ermittelt durch Interpolation von KA=34° und Gb1=54,3 und KA=35° und Gb2=53,8′

    KA=34° 17′ (=34,2833°)

        \begin{equation*} \mathit{GB}\ =\ 54,3+\frac{53,8-54,3}{35-34}\cdot (34,2833-34)\ =\ 54,158\ \approx 54,2' \end{equation*}

     

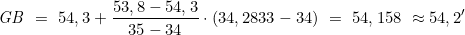
  4. Berichtigung durch Berücksichtigung des Monddurchmessers wegen Messung des Oberrandes

    Aus der Beschickungstabelle wird entnommen:

    HP 55,5′ 60,0′
    dMond 30,3′ 30,6′

    Durch Interpolation für HP = 55,7′ wird der Monddurchmesser bestimmt zu:

        \begin{equation*} d_{\mathit{Mond}}\ =\ 30,42'\ \approx \ 30,4' \end{equation*}

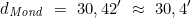
    Dieser Wert ist von der Gesamtberichtigung Gb abzuziehen:

        \begin{equation*} \sansmath \mathit{GB}\ =\ \mathit{GB}-d_{\mathit{Mond}}\ =\ 54,2-30,4=23,8' \end{equation*}

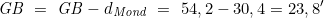
  5. Berichtigung wegen Augeshöhe:

    Für Ah = 2m sind gemäß Tabelle „Berichtigung wegen der Augeshöhe“ +3,1′ zu addieren:

        \begin{equation*} \mathit{GB}\ =\ \mathit{GB}+\mathit{Berichtigung}_{\mathit{AH}}\ =\ 23,8+3,1=26,9' \end{equation*}

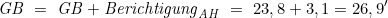
    Die Berichtigung wegen der Augeshöhe kann in einem Formblatt auch unter der „Zusatzbeschickung“ eingetragen werden.

  6. Das gesamte Rechenschema ergibt dann:

    SA 34° 20,0′
    + Ib -3,0′
    KA 34° 17,0′
    + Gb +23,8′
    + Zb +3,1′
    hb 34° 43,9′

Beschickung für Praktiker

Bedenkt man, dass die Messungenauigkeit mit dem Sextanten bei guten Messungen bereits bei ca. 1′ liegen kann, vernachlässigen wir die Nachkommastellen und reduzieren die Tabelle für Sonne und Fixsterne auf wenige Spalten und Zeilen:

Für die Beschickung des Mondes lässt sich eine solche Vereinfachung jedoch nicht herleiten, da der Einfluss der Höhenparallaxe zu groß ist.

Post Views: 438