Das Höhendifferenzverfahren

Das Höhendifferenzverfahren nach der Methode des französischen Admirals A. Blond de Marco St. Hilaire ist erstmals im Jahre 1875 veröffentlicht worden.

Es reduziert die Höhengleichen (=Kreise um den Bildpunkt) auf kleine überschaubare Ausschnitte.

Zu einem Rechenort (z.B. Koppelort) wird die theoretisch erwartete Höhe berechnet und mit der tatsächlich beobachteten Höhe verglichen. Die Differenz zwischen diesen beiden Höhen – die Höhendifferenz – lässt auf den Verlauf der Standlinie schließen.

Die Standlinie ist ein Ausschnitt der Höhengleiche und wird senkrecht zum Azimut verlaufen.

 

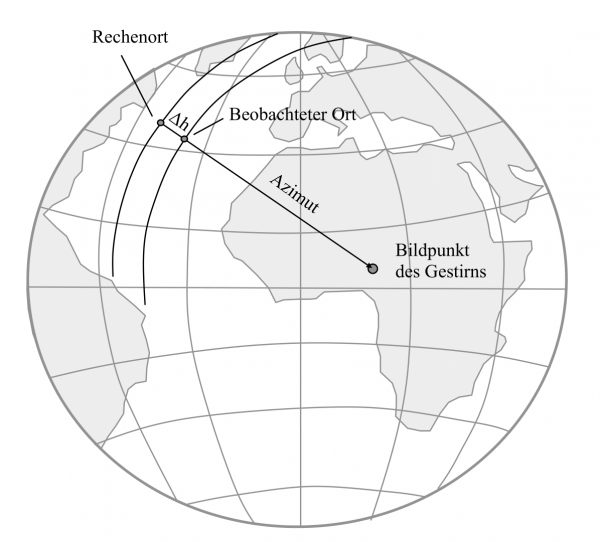
Ist die beobachtete Höhe kleiner als die berechnete Höhe, so wird der Standort weiter vom Bildpunkt entfernt sein als zuvor angenommen; ist die beobachtetet Höhe jedoch größer als die berechnete Höhe, so wird der tatsächliche Standort näher am Bildpunkt sein.

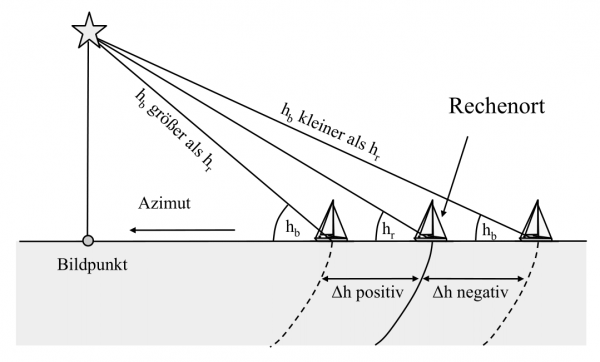
Die Höhendifferenz Δh berechnet sich zu:

∆h = Beobachtete Höhe hb – Berechnete Höre hr

Die Höhendifferenz in Winkelminuten entspricht der Distanz von angenommener zu beobachteter Standlinie in Seemeilen. Die Richtung, in die die Standlinie verschoben werden muss ist gleich dem Azimut zum Bildpunkt.

Das Verfahren lässt sich über Tafelwerke, mit Rechnern und früher mit logarithmischen Verfahren berechnen.

Ablauf

  1. Aus Chronometerzeit Chr wird die Beobachtungszeit in UT1 ermittelt.

    Chr Chronometerablesung
    + Stand Chronometerstand
    UT1 Beobachtungszeit in Universal Time 1

    Hin und wieder wird die Chronometerzeit Chr als 12stündiger Wert angegeben, so dass mit Zonenzeit ZZ und Zeitunterschied ZU ermittelt werden, ob es sich beispielsweise um 08.00 UT1 oder 20.00 UT1 handelt. Ferner können Borddatum und das GMT Datum wegen des Zeitunterschieds voneinander abweichen, so dass sich folgendes Schema ergibt:

    ZZ Datum Datum in Zeitzone
    ZZ Zonenzeit
    – ZU Zeitunterschied Zone zu Greenwich in Stunden
    GMT Greenwich Mean Time
    GMT Datum Datum in Greenich Mean Time
    Chr Chronometerablesung
    + Stand Chronometerstand
    UT1 Beobachtungszeit in Universal Time 1

  1. Nach Auswahl des Gestirns wird zur Beobachtungszeit der Greenwicher Stundenwinkel Grt berechnet und mit dem Längengrad des Rechenortes wird der Ortsstundenwinkel t bestimmt.

    Der Ortsstundenwinkel t wird vollkreisig von 0° bis 360° angegeben; eventuell sind 360° zu addieren oder zu subtrahieren.

    Sonne

    Grt v.S. Greenwicher Stundenwinkel Sonne für volle Stunde
    + Zuwachs Zuwachs des Grt für Minute und Sekunde
    Grt Greenwicher Stundenwinkel Sonne für Beobachtungszeit
    ± λ Längengrad (W: -, E: +)
    t Ortsstundenwinkel Sonne

    Fixstern

    Grt v.S. Greenwicher Stundenwinkel des Frühlingspunktes für volle Stunde
    + Zuwachs Zuwachs des Grt für Minute und Sekunde
    + Sternw Sternwinkel β des Fixsterns
    Grt Greenwicher Stundenwinkel Fixstern für Beobachtungszeit
    ± λ Längengrad (W: -, E: +)
    t Ortsstundenwinkel Fixstern

    Planet/Mond

    Grt v.S. Greenwicher Stundenwinkel des Frühlingspunktes für volle Stunde
    + Zuwachs Zuwachs des Grt für Minute und Sekunde
    + Vb Verbesserung für Mond/Planet gemäß Tabelle
    Grt Greenwicher Stundenwinkel Monat/Planet für Beobachtungszeit
    ± λ Längengrad (W: -, E: +)
    t Ortsstundenwinkel Mond/Planet

  1. Zur Beobachtungszeit UT1 wird die Deklination δ bestimmt.
    Diese wird bei Sonne, Mond und Planeten für die volle Stunde angegeben und dann mittels Verbesserung für den Beobachtungszeitpunkt berechnet:

    Sonne/Planet/Mond

    δ v.S. Deklination des Gestirns für volle Stunde
    + Vb Verbesserung für Sonne/Mond/Planet gemäß Tabelle
    δ Deklination für Beobachtungszeit

    Fixsterne

    Für Fixsterne kann die Deklination wegen der sehr langsamen Veränderung direkt für die Stunde abgelesen werden und muss nicht auf die Minute verbessert werden.

  1. Aus dem Ortsstundenwinkel, der Deklination und dem Breitengrad des Rechenortes werden die Rechenhöhe hr sowie das Azimut Az berechnet.

    Die Berechnung von hr und Az leitet sich aus dem Sphärisch-Astronomischen Grunddreieck ab:

    \sin (h)\ =\ \sin (\varphi)\cdot \sin (\delta )+\cos (\varphi )\cdot \cos (\delta )\cdot \cos(t)

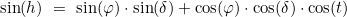
    und

    \tan (Z)\ =\ \frac{-\sin(t)}{\cos (\varphi )\cdot \tan (\delta )-\sin (\varphi )\cdot \cos(t)}

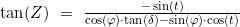
    • Ist das Azimut negativ, so sind zu Z 180° zu addieren
    • Ist der Ortsstundenwinkel kleiner als 180°, so sind zu Z weitere 180° zu addieren.

    Für diese Berechnung stehen mehrere Verfahren zur Verfügung:

    • Berechnung mit dem Taschenrechner
    • Berechnung nach Höhentafeln (z.B. PUB. 249, PUB. 229 oder andere)
    • logarithmische Verfahren (z.B. Semiversus-Verfahren)
  1. Aus der Sextantablesung SA wird die beobachtete Höhe hb nach diesem Rechenmuster bestimmt.
    SA Sextantablesung
    + Ib Indexberichtigung
    KA Kimmabstand
    + Gb Gesamtbeschickung
    + Zb Zusatzbeschickung
    hb Beobachtete Höhe
  1. Aus der beobachteten Höhe hb und und der berechneten Höhe hr wird die Höhendifferenz ∆h = hb – hr berechnet
  1. Mit Hilfe des Azimuts und der Höhendifferenz ∆h wird die Standlinie vom Rechenort aus bestimmt.
Post Views: 273